TOPIKTREND.COM, KUNCI JAWABAN SOAL Matematika Kelas 8 Halaman 93 94 Ayo Kita Berlatih 7.3 Semester 2, Esai 1-6 Lengkap – Salam Semangat, adik-adik! Mari kita belajar soal-soal dan kunci jawaban pelajaran matematika kelas 8 SMP/MTs tentang lingkaran.
Kunci jawaban matematika kelas 8 semester 2 pada bab 7 lingkaran terdapat soal “Ayo Kita Berlatih 7.3” di halaman 93, 94, dan 95.
Ayo koreksi jawaban adik-adik dengan pembahasan kunci jawaban matematika di bawah ini soal esau nomor 1-6 lengkap halaman 93 dan 94.
Pembahasan kunci jawaban matematika diharapkan dapat memudahkan adik-adik dalam memahami soal matematika kelas 8.
Dikutip dari Buku Kemdikbud Kurikulum 2013 edisi Revisi 2018, simak pembahasan kunci jawaban soal matematika kelas 8 SMP/MTs halaman 93-94 nomor 1-6 menurut Sela Dwi Utari, S. Pd., Pendidikan Matematika, FTIK-UIN Khas Jember sebagai berikut:
B. Esai
1) Lengkapilah tabel berikut.
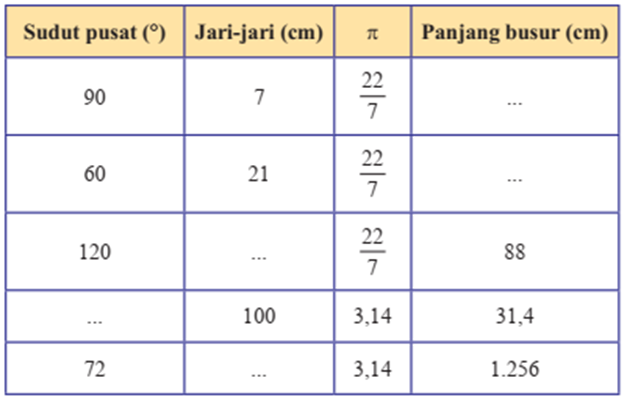
Pembahasan:
*) Diketahui: α = 90o
r = 7 cm
π = 22/7
Ditanya: Panjang busur (Pb)…?
Jawab: Pb = α/360 x 2πr
Pb = 90/360 x 2 x 22/7 x 7
Pb = 11 cm
*) Diketahui: α = 60o
r = 21 cm
π = 22/7
Ditanya: Panjang busur (Pb)…?
Jawab: Pb = α/360 x 2πr
Pb = 60/360 x 2 x 22/7 x 21
Pb = 22 cm
*) Diketahui: α = 120o
Pb = 88 cm
π = 22/7
Ditanya: r…?
Jawab: Pb = α/360 x 2πr
88 = 120/360 x 2 x 22/7 x r
88 = 1/3 x 44/7 x r
r = (88 x 3 x 7)/44
r = 42 cm
*) Diketahui: Pb = 31,4
r = 100 cm
π = 3,14
Ditanya: α …?
Jawab: Pb = α/360 x 2πr
31,4 = α /360 x 2 x 3,14 x 100
31,4 = α /360 x 628
α = (31,4 x 360) x31,4
α = 18o
*) Diketahui: α = 72o
Pb = 1.256 cm
π = 3,14
Ditanya: r…?
Jawab: Pb = α/360 x 2πr
1.256 = 72/360 x 2 x 3,14 x r
1.256 = 1/5 x 6,28 x r
r = (1.256 x 5)/6,28
r = 6.280/6,28
r = 1.000 cm
2) Lengkapilah tabel berikut.
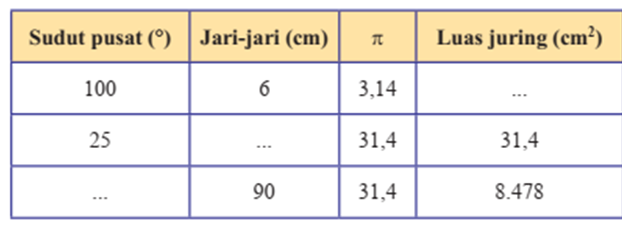
Pembahasan:
*) Diketahui: α = 100o
r = 6 cm
π = 3,14
Ditanya: Luas juring (Lj)…?
Jawab: Lj = α/360 x πr2
Lj = 100/360 x 3,14 x 6 x 6
Lj = 11.304/360
Lj = 31,4
*) Diketahui: α = 25o
Lj = 31,4 cm
π = 3,14
Ditanya: r…?
Jawab: Lj = α/360 x πr2
31,4 = 25/360 x 3,14 x r2
r2 = (31,4 x 360)/(25 x 3,14)
r2 = 11.304/78,5
r2 = 144
r = 12
*) Diketahui: Lj = 8.478
r = 90 cm
π = 3,14
Ditanya: α …?
Jawab: Lj = α/360 x πr2
8.478 = α/360 x 3,14 x (90)2
8.478 = α/360 x 3,14 x 8.100
α = (8.478 x 360)/(3,14 x 8.100)
α = 3.052.080/25.434
α = 120o
3) Tentukan luas juring lingkaran yang diketahui sudut pusatnya 70o dan jari-jarinya 10 cm.
Pembahasan:
Diketahui: α = 70o
r = 10 cm
π = 3,14
Ditanya: Luas juring (Lj)…?
Jawab: Lj = α/360 x πr2
Lj = 70/360 x 3,14 x 10 x 10
Lj = 7/36 x 314
Lj = 2.198/36
Lj = 61,05 cm
4) Tentukan panjang busur lingkaran yang diketahui sudut pusatnya 35o dan jari-jarinya 7 cm.
Pembahasan:
Diketahui: α = 35o
r = 7 cm
π = 22/7
Ditanya: Panjang busur (Pb)…?
Jawab: Pb = α/360 x 2πr
Pb = 35/360 x 2 x 22/7 x 7
Pb = (35 x 44)/360
Pb = 1.540/360
Pb = 4,27 cm
5) Lingkaran A memiliki jari-jari 14 cm. Tentukan sudut pusat dan jari-jari suatu juring lingkaran lain agar memiliki luas yang sama dengan lingkaran A.
Pembahasan: Lj2 = L1
α/360 x πr22 = πr2 (π bisa dicoret)
α/360 x r22 = (14)2
α/360 x r22 = 196
misal r2 = 28
maka, α/360 x (28)2 = 196
α/360 = 196/784
α/360 = ¼
α = 360/4 = 90o
Jadi juring lingkaran memiliki α = 90o dan r = 28 cm
6) Buatlah lingkaran A dengan jari-jari tertentu, sedemikian sehingga luasnya sama dengan juring pada lingkaran B dengan sudut pusat dan jari-jari tertentu. Jelaskan.
Pembahasan:
Lingkaran A = Luas juring B
πrA2 = α/360 x πrB2 (π bisa dicoret)
rA2 = α/360 x rB2
Misal rA2 = 7 cm dan rB2 = 21 cm
Maka,
72 = α/360 x 212
α = (49 x 360)/441
α = 40o
Jadi, agar luas lingkaran A dan luas juring B sama, rA 7 cm, rB = 21 cm dengan α = 40o
Demikian dulu pembahasan kunci jawaban soal matematika Kelas 8 SMP/MTs Ayo Kita Berlatih 7.3 halaman 93-94 esai nomor 1-6. Semoga membantu.
Disclaimer:
1.Konten ini disajikan dan dibuat bertujuan agar dapat membantu para orang tua dalam membimbing anak selama belajar.
2.Pembahasan kunci jawaban ini bersifat terbuka, baik siswa dan orang tua dapat mengeksplorasi jawaban yang lebih baik.
3.Artikel ini tidak mutlak menjamin kebenaran jawaban.***